As the spiral groove is cut into the master lacquer, the cutting radius — defined as the distance from the stylus to the center of the disc — gradually decreases. This reduction in cutting diameter can lead to increased information loss, primarily due to the limitations in groove tracing accuracy
These are inherent physical limitations resulting from the continuous decrease in peripheral speed.
During cutting, the master lacquer rotates at a constant angular velocity. The stylus carves the groove at a specific point, which can be represented as the end of a segment r (the cutting radius), with the other end anchored at the center of the disc.
Peripheral velocity refers to the linear speed of a point traveling along a circular path, located at a distance r from the center of rotation:
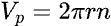
where 2π indicates the full circumference (360°), r the radius, and n the rotational speed of the lacquer. The peripheral velocity is generally expressed in cm/s, therefore — if the standard record speed in rpm is used — care must be taken to divide by 60.
Since the stylus vibrates with amplitudes and frequencies that are independent of both the cutting radius and the rotational speed, a decrease in radius means that the same amount of vibrational information is recorded over a smaller surface area. As a result, the groove becomes more densely packed.
This increased density can lead to two main types of losses, which become more significant as the peripheral velocity 𝑉𝑝 decreases:
- cutting losses: high frequencies, which involve rapid stylus movements and therefore high groove velocities, are more difficult to accurately cut and are often lost or diminished;
- tracking losses: the playback stylus may struggle to follow the tightly spaced undulations of the groove, especially at high frequencies¹.
Physically, these losses are unavoidable. Acoustically, their impact can range from subtle to pronounced, depending on the track’s frequency content, the recording context, and the overall volume. When audible, the result is a muffled, less defined sound with a noticeable loss in high-frequency detail.
The issue is exacerbated at higher cutting volumes, as increased amplitude also leads to more pronounced groove curvature (see "acceleration" below).
This problem is well known and, being rooted in physical limitations, offers few solutions beyond strategic planning:
- track sequencing: arrange the order of the tracks so that those least affected by high-frequency loss — such as mono-instrumental pieces with limited modulation — are placed toward the end of each side;
- early termination: if feasible in terms of volume and duration, conclude the cut while the cutting radius is still relatively large;
- higher speed cutting: if the program duration and volume permit, cut at 45 rpm instead of 33⅓ rpm. The higher rotational speed increases the peripheral velocity, mitigating the effects of the decreasing radius.
Acceleration
Another important aspect of the cutting dynamics involves the excessive curvature of the groove.
Attention is given to curvature because it must not fall below the radius of the tip of the stylus that traces the groove. If this happens, in fact, the stylus — which has a conical tip — no longer remains perfectly in contact with the walls of the groove and does not reproduce the same vibrations as the cutting stylus, according to the geometry of the groove itself. As a result, the sound produced is no longer faithful to what was recorded, and ends up being more or less distorted.
The curvature g is the ratio between the square of the peripheral velocity Vp and the peripheral acceleration b. The curvature is acceptable as long as it does not fall below the diameter of the playback stylus.
Spherical styli have a tip radius of 15–20 µm. This means they always make full contact with the bottom of a straight groove, as long as the groove is at least 30–40 µm wide. This is a common characteristic of practically all commercially available styli.
We can therefore define g as:
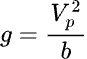
b is directly proportional to the current supplied by the amplifier to the coils and to the magnetic field, and it is not related to frequency. A slightly more complex calculation comes into play here, which involves Lorentz’s law. For practical purposes, these calculations are not particularly useful, also because they would require knowing certain parameters of the cutterhead which are almost never available. However, there are empirical values provided by manufacturers that can be used for rough estimations.
For example, the maximum theoretical acceleration produced by a system using an SAL74 amplifier and SX74 cutterhead is 47,500 m/s² at a continuous current of 8A. Clearly, this is a theoretical value, not practically achievable.
We can use this value to look at two examples of groove curvature.
Example 1
With a rotation speed of 33.33 rpm, a cutting radius of 8 cm, and a current of 0.5A (which might correspond, for instance, to the peak of an “S” sound in a medium volume voice, post-RIAA equalization), we obtain:
The peripheral speed is:
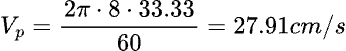
and the groove curvature is:
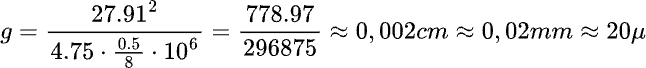
that is, a traceable curvature without issues.
Example 2
If the same cut is moved closer to the center of the record (r=6 cm) at an even higher volume, and there is a peak current of 1A,
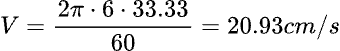
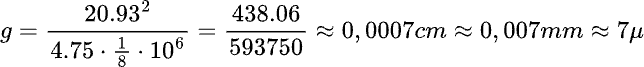
then the curvature becomes too tight to be accurately tracked by the stylus, causing distortion.
An interesting calculation is the one used to determine the maximum allowable current to avoid going below 15µm of minimum curvature, when the cutting radius is 6 cm. To calculate this, we need to solve the previous equation with respect to b, knowing that in this case g is 15µm.
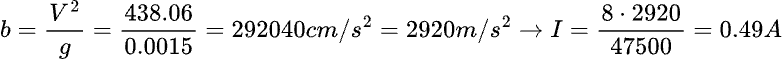
It can therefore be concluded that a larger cutting radius — and consequently a higher peripheral velocity — significantly increases the value of g, while a higher current (which increases the value of b) reduces it.
Although the peripheral acceleration b has no inherent connection to frequency, it is important to emphasise that when moving into a strongly equalised context like the RIAA, the currents generated by low, medium and high-frequency signals are obviously strongly unbalanced pre- and post-equalisation. This is because current, when resistance remains constant, is directly proportional to voltage, and therefore to the amplitude of the signal.
In the case of RIAA equalization, it goes from -19.6 dB at 20 Hz to +19.6 dB at 20 kHz. As a result, mid/high frequencies can generate fairly high currents for the cutterhead, which must be taken into account both in terms of the actual cutting process (groove curvature and velocity) and in terms of the cutterhead’s potential overheating.
Until the early 1970s, cutterheads could handle a power of 100W per channel and temperatures up to around 120°C. Later on, thanks to the use of new materials, this increased to about 200°C.
The cutter head is protected from overcurrent by a "circuit breaker" in each of the two channels. Until the early 1970s, it was sufficient to limit the power of the cutting amplifier; following the introduction of very powerful amplifiers (600W per channel), capable of causing — if over-driven — irreparable damages to the cutter heads, it became clear that such a circuit was too slow, and thus a different approach was developed, focused on the temperature of the coils. Due to the specific design of the circuit, it wasn‘t possible to use a real temperature monitoring, hence the temperature is estimated according to the measured resistance of the coils, which under normal conditions (SX74 heads) is 4.7Ω, while at 200°C rises up to 8.2Ω. The use of very fast reed relays (<1ms) allows for the instantaneous interruption of the current flow when necessary (2).
Nevertheless, the temperature of the head can also be cooled by means of a constant and adjustable flow of helium.
To attenuate the signal components that can generate current peaks (loud “S” sounds, analogue hi-hats, and similar) without having to modify the master equalisation, the established practice is to use one or more de-essers in the signal processing chain before it reaches the recording amplifier.
1 Larry Boden, Basic Disc Mastering, USA, 1981
2 O. Kern and E. Weiss, Essential Equipment for the Transmission of High Peak Levels in the Disk-Cutting System SAL 74/SX 74, JAES vol. 23, n° 9, USA, November 1975