Come funzionano i solchi

La testina di incisione, come abbiamo visto in precedenza, trasforma la corrente che arriva alle sue bobine in vibrazioni dello stilo di incisione. Può essere considerata come un elettromagnete, simile a quelli che si trovano nei sistemi telefonici convenzionali, ma con una potenza maggiore in gioco.

Oggi, nelle testine stereo, le bobine sono posizionate ad angoli di ±45° rispetto al piano di modulazione, cioè alla superficie del disco master. Di conseguenza, sono distanziate di 90° l’una dall’altra. Questa configurazione fa sì che i solchi che vengono incisi contengano sempre informazioni sia verticali che laterali¹.

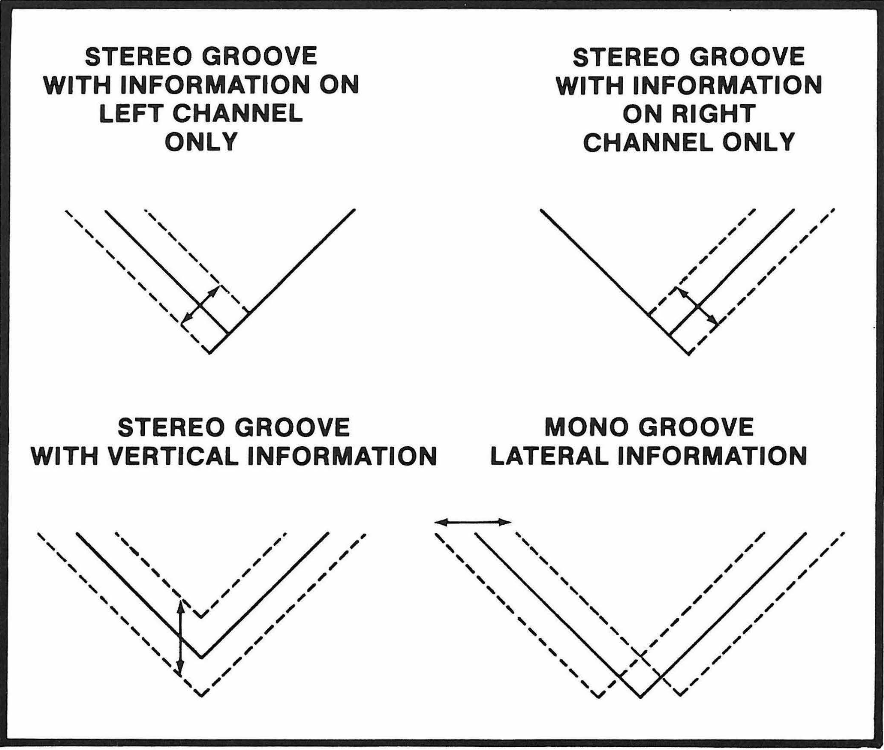
Questo sistema, introdotto per la prima volta dalla Westrex negli Stati Uniti oltre 50 anni fa, è diventato rapidamente lo standard del settore. All’epoca, i dischi mono erano ancora i più diffusi, e la rotazione di 45° dell’asse verticale ha consentito per la prima volta di incidere un segnale stereo nel quale i solchi incisi hanno una geometria abbastanza lineare e facilmente riproducibile. Cosa che non avverrebbe, ad esempio, se uno dei due canali facesse muovere lo stilo in senso verticale e l'altro in orizzontale.

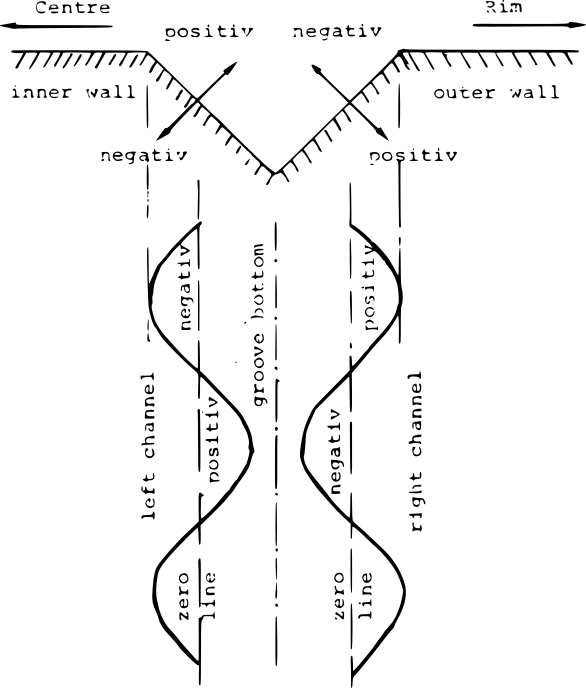
La figura precedente² schematizza la logica di incisione di un solco, ipotizzando che la testina si muova da destra a sinistra, verso il centro del disco.

Si può notare che il canale destro viene sempre inciso nella parte del solco rivolta verso il bordo del disco. Inoltre le polarità dei due canali sono opposte:

• sul canale destro, la polarità "+" fa scendere in profondità lo stilo, lungo l‘asse inclinato di 45°, e viceversa;
• sul canale sinistro, ciò accade con la polarità "-".

Quindi, se si incide un segnale stereo monofrequenza con la stessa ampiezza in entrambi canali, vi saranno solo escursioni laterali dello stilo, che seguono la forma d'onda.

Se invece il segnale ha ampiezza diversa sui due canali, oltre all‘escursione laterale ci sarà anche un'escursione verticale più o meno contenuta, che produrrà una variazione della profondità del solco.

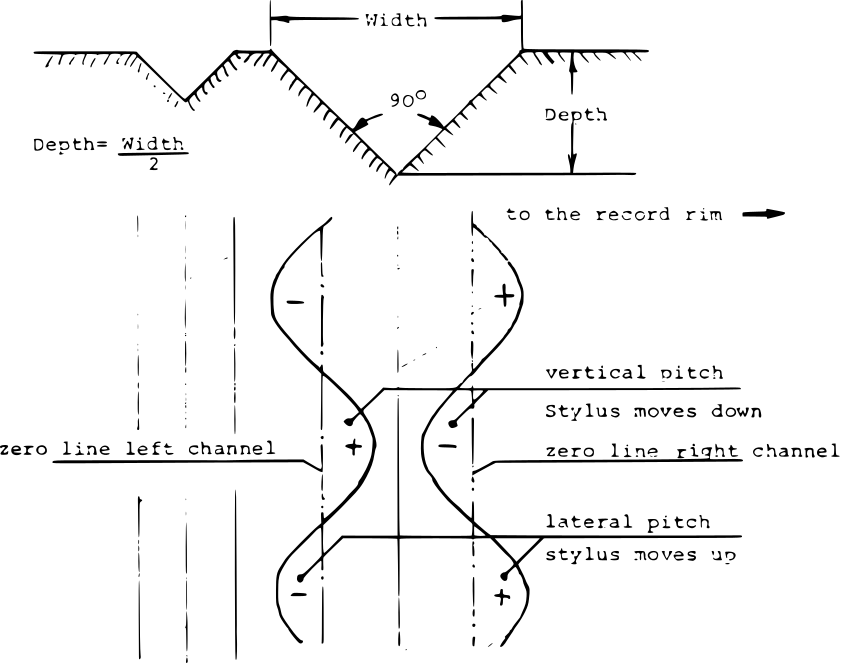
Come si può notare nella figura precedente³, chiamate VL e VR le tensioni modulate dei 2 canali, ricordando che esse hanno polarità opposte, si ha che:

• quando (±VL) + (±VR) diminuisce, lo stilo incide con una profondità maggiore;
• quando (±VL) + (±VR) aumenta, lo stilo incide con una profondità minore.

Tutto questo è facile da osservare quando viene inciso un segnale in cui è presente una sola frequenza. Quando il segnale è composito, le varie frequenze si accavallano l'una sull'altra. L'effetto più visibile, a livello di solco, sarà dato dalla frequenza prevalente, ma anche altri aspetti del segnale saranno visibili: al microscopio, ma talvolta anche ad occhio nudo.

Ad esempio:

• solco con modulazione laterale ampia: basse frequenze (bassa e ampia velocità della vibrazione dello stilo, vedi "costanti di tempo" qui sotto)
• solco seghettato: alte/altissime frequenze (alta velocità di vibrazione dello stilo, vedi "costanti di tempo" qui sotto)
• solco "puntinato": variazioni repentine di profondità, probabilmente per forte differenza stereo sulle medio/basse frequenze (azione asincrona delle bobine)

Chiaramente, in un segnale composito i tre esempi di cui sopra possono anche comparire insieme, nella stessa sezione di un qualunque solco.

Costanti di Tempo

"Costante di tempo" è un termine utilizzato, anche scientificamente, in diversi settori, e non ha un significato univoco. Nel nostro caso, indica il tempo di risposta tipico di un circuito elettrico, attraversato dal segnale di linea, in relazione ad una determinata frequenza del segnale stesso.

Quando parliamo di tempo di risposta noi presupponiamo, appunto, una risposta, cioè la produzione di un effetto che scaturisce dal circuito e dalle sue componenti. Abbiamo visto in precedenza che l'amplificatore di incisione fornisce corrente alle bobine della testina. Questa corrente ha l'effetto primario di generare induttanza, e l'effetto secondario di far vibrare lo stilo di incisione. Le caratteristiche di queste vibrazioni non dipendono solo dalla quantità di corrente, ma anche dalla frequenza e dalla costante di tempo ad essa associata.

Se incidiamo un segnale composto da una forma d'onda con frequenza di 1kHz, lo stilo vibra 1000 volte al secondo. In base alla relazione tra frequenza e periodo (T=1/f), quest’ultimo è di 1ms, pertanto la sequenza ciclica di queste 1000 vibrazioni si ripeterà ogni 1ms.

Il volume del nostro segnale determinerà quanto ampia sarà la vibrazione, ma non influirà su frequenza e periodo. Quindi lo stilo vibrerà sempre e comunque 1000 volte al secondo.

Allo stesso modo, se la forma d’onda ha una frequenza di 6kHz, le vibrazioni al secondo saranno 6000, ed il periodo sarà più breve (0.17ms).

Si può quindi affermare che la velocità del solco, cioè il tempo nel quale la vibrazione dello stilo raggiunge la sua massima escursione e ritorna al suo punto di partenza, è direttamente proporzionale alla frequenza prevalente del segnale.

Inoltre, indipendentemente dal volume del segnale, le basse frequenze producono vibrazioni più ampie rispetto alle frequenze medie e alte, e le frequenze medie producono vibrazioni più ampie rispetto alle frequenze alte.

Infatti, se vengono trascritte allo stesso volume una forma d’onda sinusoidale da 1kHz e una da 200Hz, quest’ultima genera 1/5 delle vibrazioni al secondo (200) rispetto alla prima, ma poiché il volume è lo stesso, queste 200 vibrazioni al secondo hanno escursioni laterali e verticali 5 volte più ampie rispetto alle 1000, perciò richiedono un po’ più di tempo per compiersi dall’inizio alla fine.

Quindi, a parità di volume, minore è la frequenza, maggiore è l'ampiezza delle vibrazioni dello stilo, sia per quanto riguarda l‘escursione orizzontale che per quanto riguarda quella verticale.

Ogni frequenza ha associata una propria costante di tempo, che viene indicata con la lettera greca "tau":

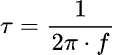
la costante di tempo è inversamente proporzionale alla frequenza, il che significa che le alte frequenze hanno costanti di tempo più piccole (veloci) e le basse frequenze viceversa.

Convertendo i secondi in microsecondi, si ricava la seguente equazione condizionale:

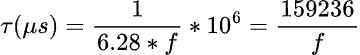
Questa equazione, se applicata alla frequenza di 1kHz, dà un risultato di 59.23µs, e alla frequenza di 200Hz dà un risultato di 796.18µs.

Ripetendo lo stesso calcolo per gli estremi della gamma di frequenze riproducibili da una testina (normalmente, 20Hz e 20kHz), si ottiene un risultato di 7957.75µs a 20Hz, e di 7.95µs a 20kHz.

A questo punto si può cominciare ad intuire il perché della necessità dell'equalizzazione RIAA, a cui abbiamo accennato in precedenza.

Infatti, possiamo osservare che la costante di tempo dei 20Hz risulta 1000 volte più alta di quella dei 20kHz. In un contesto simile, sarebbe altamente inefficiente — in assenza di un‘equalizzazione correttiva — incidere su disco un segnale di linea contenente l’intero spettro di frequenze, poiché le basse frequenze causerebbero escursioni orizzontali e verticali troppo grandi dello stilo, e l‘opposto accadrebbe con le alte frequenze, rendendo il rapporto segnale/rumore inaccettabile.

La soluzione è quindi quella di attenuare le basse frequenze ed enfatizzare le alte frequenze in registrazione, per sopperire a questa sproporzione. Un'equalizzazione speculare dovrà essere poi inserita nel circuito “phono” di riproduzione del segnale, per ripristinare la corretta risposta in frequenza.

La Curva RIAA

Negli anni ’60, la Recording Industry Association of America (RIAA) ha standardizzato alcune delle curve di equalizzazione proposte nel corso degli anni precedenti nella “curva RIAA" (vedi figura seguente), che rimane ad oggi la curva standard nel circuito di amplificazione “Phono”.

La funzione dB(f) ha come componenti, oltre alla frequenza f, tre costanti di tempo:

 

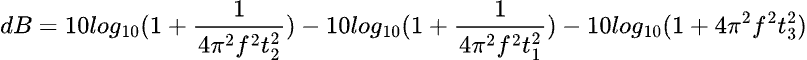
dove

• t1 è la costante di tempo delle alte frequenze (≈75µs);
• t2 è la costante di tempo delle medie frequenze (≈318µs);
• t3 è la costante di tempo delle basse frequenze (≈3180µs).

La curva è centrata sui 1000Hz. Quella della figura qui sopra è la curva RIAA di riproduzione. Un sistema di incisione, ovviamente, registra il suono con un'equalizzazione diametralmente opposta, cioè con le basse frequenze attenuate e le alte frequenze enfatizzate. Ovvero, semplificando:

in registrazione:

• -19.6dB a 20Hz
• 0dB a 1000Hz
• +19.6dB a 20Khz

in riproduzione:

• +19.6dB a 20Hz
• 0dB a 1000Hz
• -19.6dB a 20kHz

I circuiti di equalizzazione RIAA sono costituiti da una combinazione di filtri passa alto/passa basso. Oggi vengono quasi sempre implementati tramite reti di resistenze, condensatori e amplificatori operazionali.

Escursione verticale

Tra le due componenti in cui possiamo scomporre le vibrazioni dello stilo (escursione orizzontale e verticale), quella da tenere d'occhio è certamente l'escursione verticale.

Nell'ipotesi in cui:

• la differenza tra (±VL) e (±VR) è grande;
• il segnale ha un volume alto;
• la costante di tempo della frequenza prevalente è alta,

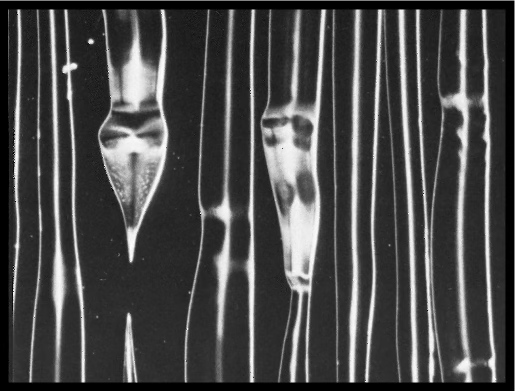
allora il solco può diventare prima molto profondo, e subito dopo molto sottile.

Difficilmente il solco può diventare così profondo da far sì che lo stilo tocchi l'anima di alluminio del disco master, danneggiandosi irrimediabilmente. Però un solco molto largo prima, e molto sottile dopo, può generare qualche rumorino in riproduzione. Inoltre, se diventa troppo sottile, può non essere nemmeno tracciabile dalla puntina del giradischi. Il raggio medio di uno stilo di riproduzione è di 15µ, pertanto la larghezza del solco non dovrebbe mai scendere sotto i 30µ.

Va detto che la profondità del solco durante l'incisione è il prodotto di due fattori ben distinti:

• la profondità di base, impostata all'inizio dell'incisione, che dipende sia da regolazioni di tipo meccanico (sulla sospensione a cui è agganciata la testina), sia dall'azione elettromagnetica del moving coil della testina, la cui corrente viene regolata con un potenziometro, e che è lo strumento "di precisione" con cui si regola la profondità di base del solco, senza alcun segnale presente;
• l'escursione verticale, che si somma o si sottrae alla profondità di base quando il solco è modulato, come risultante della differenza tra (±VL) e (±VR).

Senza alcun intervento sul segnale, nei casi peggiori la situazione potrebbe essere quella della figura sottostante⁴.

Per evitare o contenere questi problemi, il contenuto del segnale viene corretto prima che questi arrivi all’amplificazione. Tra gli interventi più usati vi sono:

• filtro ellittico/mono-maker: è un filtro a banda passante con curva molto ripida, caratterizzato da un calcolo dei poli e degli zeri estremamente complesso, volto a  minimizzare l'errore sia al di sopra che al di sotto della frequenza di crossover. Il segnale viene processato in modo che la banda passante abbia un'immagine stereo nulla, e quindi non produca alcuna escursione verticale dello stilo durante l'incisione. In questo modo si vanno eliminare le forti escursioni verticali dovute alla compresenza di alte differenze tra (±VL) e (±VR) e alte costanti di tempo alte, ma al tempo stesso si interviene sulla stereofonia in maniera contenuta, cioè solo fino ad una determinata frequenza. Questo filtro viene utilizzato da oltre 50 anni ed è spesso integrato come componente sempre attivo nei sistemi di incisione professionale. E' sicuramente il sistema più efficace, ma è anche abbastanza invasivo.
• equalizzazione MS: consente di equalizzare separatamente la componente mono (cioé quella al centro dell’immagine stereo) e la componente stereo (alle estremità) del segnale. E’ particolarmente utile quando si individua la frequenza attorno alla quale si genera la variazione di profondità del solco. Si equalizza solo la componente stereo intorno alla frequenza di interesse, quel tanto che basta per attenuare la variazione stessa. Questa soluzione può produrre un risultato efficace e molto difficile da individuare all’ascolto, se confrontato con la registrazione originale.

1, 3 Larry Boden, Basic Disc Mastering, USA 1981
2, 4 Struck, Polygram Pitch Control IV user manual, internal files, UK-Europe 1977-82